Excel で切手組み合わせ問題を整数計画問題として解く
2025/09/06 12:17
その内部では整数計画問題ソルバである GLPK (Gnu Linear Programming Kit) を使って最適解を求めていますが、
同様のことを Microsoft Excel と付属ソルバを使って求めてみようと思います。
準備
- Excel のオプション -> アドイン -> 管理 -> Excel アドイン -> ソルバーアドイン があるのを確認 -> 設定ボタンをクリック
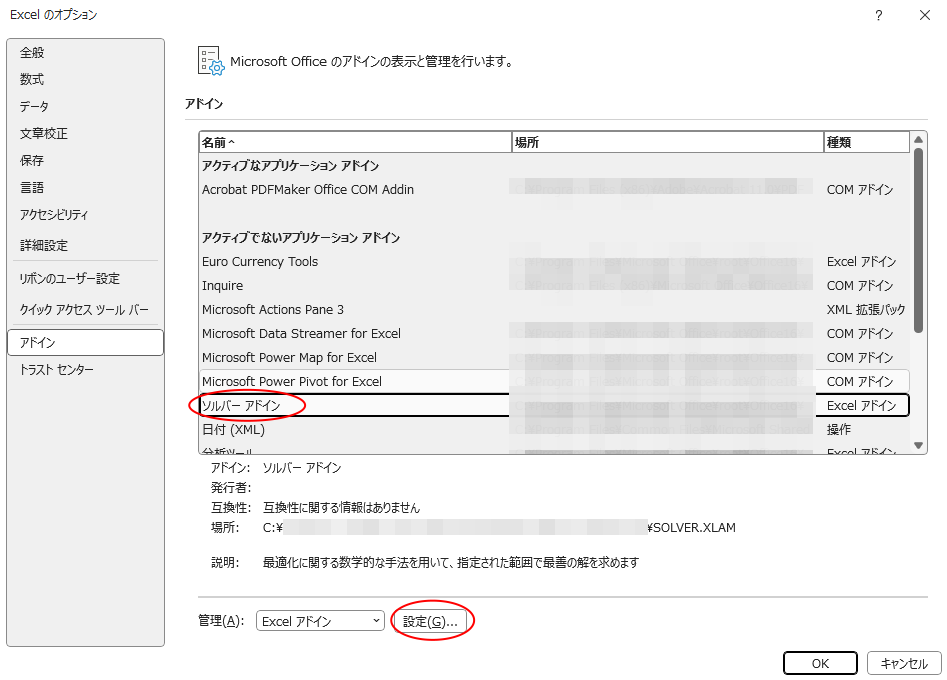
- ソルバーアドイン にチェック -> OK ボタンをクリック
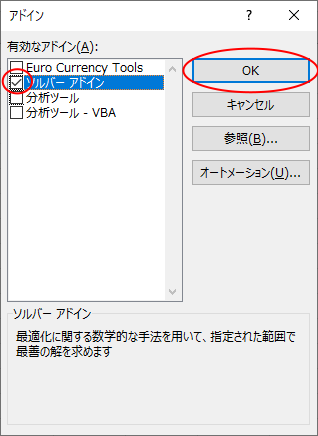
入力フォーマットや数式の入力
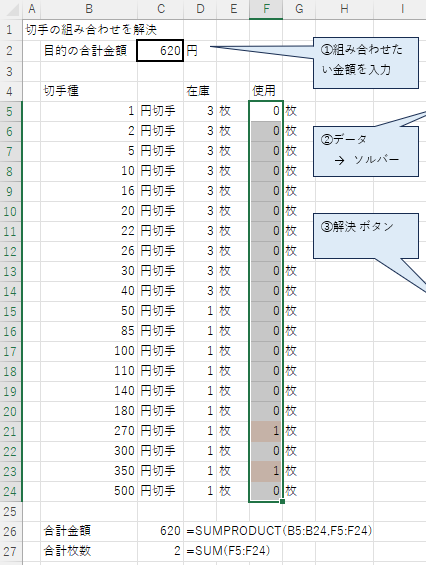
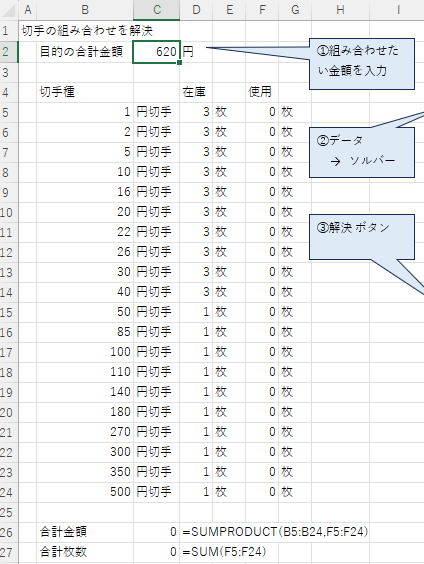
- 例えば次のようなフォーマットを用意します。
Excel ファイルは こちら
- C2 セルに 組み合わせたい金額を入力します
- B5 セルから B24 セルには切手の単価を入力します。とりあえず現在発売中の切手の金額を入力します。
- D5 セルから D24 セルに手持ちの枚数を入力します。
- F5 セルから F24 セルに後ほど結果が代入されます。なんでもいいのですが、とりあえず 0 で埋めておきます。
- C26 セルは組み合わせ試行中の合計金額を表します。数式 =SUMPRODUCT(B5:B24,F5:F24) を入力します。この数式は (単価×枚数) の総和を意味します。
- C27 セルは組み合わせ試行中の合計枚数を表します。数式 =SUM(F5:F24) を入力します。これがこの問題の最小化させたい目的関数となります。
ソルバーの設定
- メニューの データ タブ -> 分析 -> ソルバー をクリック

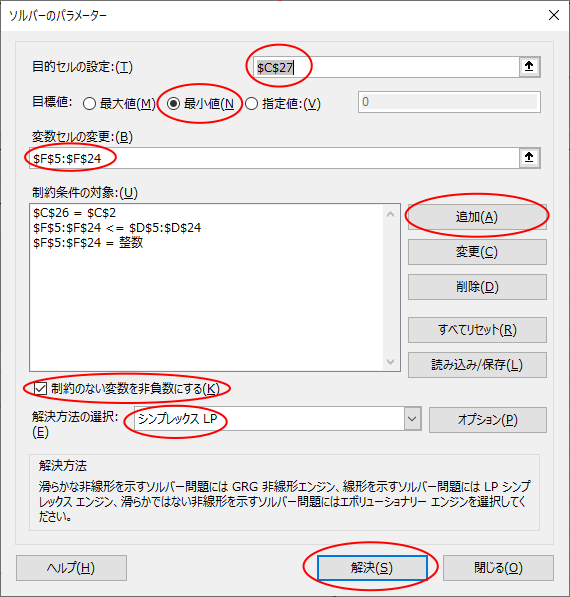
- 目的セルを C27 に設定します。このセルは合計枚数を示すものです。
- 目標値は 最小値 を選択します。合計枚数を最小にする解を得たいからです。
- 変数セルは F5:F24 にします。ソルバーによってこの範囲に各切手の枚数が代入されていきます。
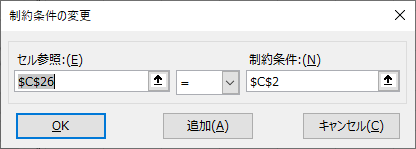
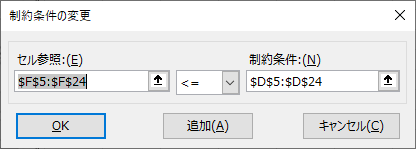
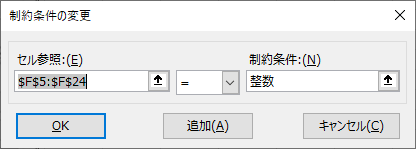
- 制約条件の対象 に3つ条件を追加します。
- 制約のない変数を非負数にする にチェックします。切手の使用枚数はマイナスにはならないからです。
- 解決方法の選択 では シンプレックスLP を選択します。ここで解決したい問題が線形を示す問題だからです。
- 最後に 解決 ボタンをクリックします。
結果を読む
- 「整数解が見つかりました」と出たら成功です。
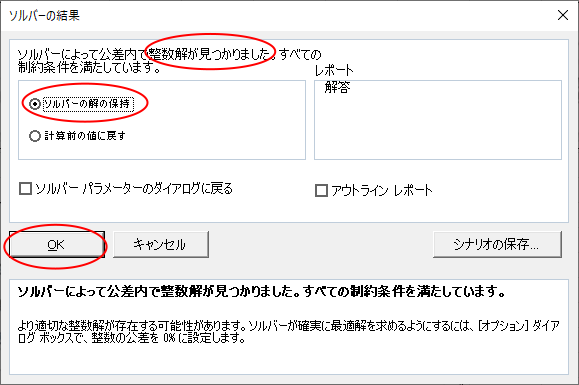
- 「実行可能解が見つかりませんでした」と出たら、手持ちの切手では合計金額ちょうどの組み合わせが作れなかったということです。
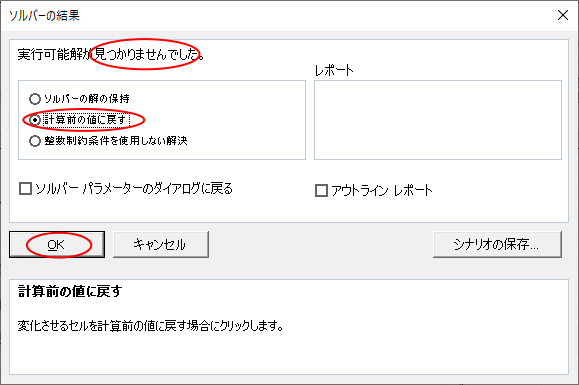
- 計算前の値に戻す を選択して OK ボタンをクリックして戻り、在庫枚数などの条件を見直しましょう。
参考
- Wikipedia日本語版「整数計画問題」: https://ja.wikipedia.org/wiki/%E6%95%B4%E6%95%B0%E8%A8%88%E7%94%BB%E5%95%8F%E9%A1%8C
- Wikipedia日本語版「切手問題」:https://ja.wikipedia.org/wiki/%E5%88%87%E6%89%8B%E5%95%8F%E9%A1%8C